2.3 Límites laterales.

Límites laterales.

Objetivo
Con este blog pretendemos que los/as alumnos/as descubran la belleza de la matemáticas, que la sepan apreciarla en las formas de la naturaleza, en el arte, en su día a día etc.

Límites laterales

Hasta el momento hemos visto límites de funciones cuyo trazo es continuo, sin cortes o saltos bruscos. Sin embargo, existen algunas funciones que presentan algunas discontinuidades, llamadas funciones discontinuas y que estudiaremos en el tema continuidad de funciones. Nos dedicaremos ahora a estudiar los límites en este tipo de funciones.
Consideremos la siguiente representación gráfica de una función , en la que existe una discontinuidad cuando :

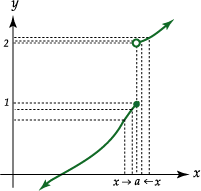notemos que cuando  tiende hacia "a" por la derecha de "a" la función tiende a 2, pero cuando  tiende hacia "a" por la izquierda de "a", la función tiende hacia 1.

Escribimos  para indicar que  tiende hacia "a" por la derecha, es decir, tomando valores mayores que "a". Similarmente  indica que  tiende hacia "a" por la izquierda, o sea, tomando valores menores que "a". Utilizando ahora la notación de límites, escribimos  y . Estos límites reciben
el nombre de límites laterales; el límite por la derecha es 2 y el límite por la izquierda es 1. 
Ejemplo:
Determinaremos los límites en los puntos de discontinuidad de la función  cuya representación gráfica es la siguiente:

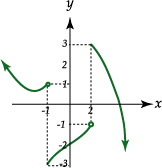Se tiene que:  y   y

Bibliografía